Tổng hợp 7 thuật toán sắp xếp phổ biến trong C++

Bài viết được sự cho phép của tác giả Khiêm Lê

Thuật toán sắp xếp là lời giải của bài toán sắp xếp. Mục đích của việc sắp xếp chính là giúp ta có cái nhìn tổng quan hơn về những dữ liệu là cơ sở cho các giải thuật nâng cao với hiệu suất cao hơn.

Ví dụ như khi thực hiện tìm kiếm, thuật toán tìm kiếm nhị phân có độ phức tạp thời gian là O(log(n)) và ổn định, nhưng thuật toán này chỉ áp dụng được với dãy đã được sắp xếp. Vậy khi này, bạn có thể thực hiện sắp xếp trước sau đó áp dụng thuật toán tìm kiếm nhị phân.

Trong bài viết này, TopDev sẽ giới thiệu đến các bạn một số thuật toán sắp xếp trong C++ phổ biến nhất mà lập trình viên nào cũng nên biết. Hãy cùng bắt đầu thôi!

Tham khảo thêm các vị trí tuyển dụng lập trình C++ hấp dẫn nhất.

Định nghĩa thuật toán sắp xếp trong C++

Thuật toán sắp xếp – hàm sort() trong C++ được định nghĩa là một hàm trong thư viện <algorithm> của C++ dùng để sắp xếp các phần tử trong một phạm vi (range) nhất định theo thứ tự tăng dần hoặc theo một tiêu chí cụ thể do người dùng định nghĩa.

Hàm sort C++ được cài đặt sẵn là hàm intro - sort, đây là sự kết hợp của 2 thuật toán sắp xếp rất hiệu quả là quick sort và heap sort. Hàm này mặc định sắp xếp các giá trị tăng dần, nếu muốn sắp xếp giảm dần cần thêm tham số greater().

Độ phức tạp của hàm sort() là O(NlogN)

Xem thêm: Lập trình C++ cơ bản

Ví dụ minh họa hàm sort C++

#include <iostream>
#include <algorithm>
#include <vector>

int main() {
    std::vector<int> vec = {5, 2, 9, 1, 5, 6};

    // Sắp xếp tăng dần
    std::sort(vec.begin(), vec.end());

    // In kết quả
    for (int i : vec) {
        std::cout << i << " ";
    }
    return 0;
}

Các thuật toán sắp xếp trong C++

Các hàm sort trong C++ phổ biến:

Sắp xếp nổi bọt (Bubble Sort)
Sắp xếp chọn (Selection Sort)
Sắp xếp chèn (Insertion Sort)
Sắp xếp nhanh (Quick Sort)
Sắp xếp trộn (Merge Sort)
Sắp xếp vun đống (Heap Sort)
Sắp xếp đếm (Counting Sort)

Hàm sắp xếp nổi bọt (Bubble Sort)

Sắp xếp nổi bọt hay bubblesort là thuật toán sắp xếp đầu tiên mà mình giới thiệu đến các bạn và cũng là thuật toán đơn giản nhất trong các thuật toán mà mình sẽ giới thiệu, ý tưởng của thuật toán này như sau:

Duyệt qua danh sách, làm cho các phần tử lớn nhất hoặc nhỏ nhất dịch chuyển về phía cuối danh sách, tiếp tục lại làm phần tử lớn nhất hoặc nhỏ nhất kế đó dịch chuyển về cuối hay chính là làm cho phần tử nhỏ nhất (hoặc lớn nhất) nổi lên, cứ như vậy cho đến hết danh sách Cụ thể các bước thực hiện của giải thuật này như sau:

Gán i = 0
Gán j = 0
Nếu A[j] > A[j + 1] thì đối chỗ A[j] và A[j + 1]
Nếu j < n – i – 1:
- Đúng thì j = j + 1 và quay lại bước 3
- Sai thì sang bước 5
Nếu i < n – 1:
- Đúng thì i = i + 1 và quay lại bước 2
- Sai thì dừng lại

Thật đơn giản đúng không nào, chúng ta hãy cùng cài đặt thuật toán này trong C++ nha.

void BubbleSort(int A[], int n)
{
    for (int i = 0; i < n - 1; i++)
        for (int j = 0; j < n - i - 1; j++)
            if (A[j] > A[j + 1])
                swap(A[j], A[j + 1]); // đổi chỗ A[j] và A[j + 1]
}

Sắp xếp nổi bọt là một thuật toán sắp xếp ổn định. Về độ phức tạp, do dùng hai vòng lặp lồng vào nhau nên độ phức tạp thời gian trung bình của thuật toán này là O(n²).

Các bạn có thể xem mình trình bày ý tưởng của giải thuật này trong bên dưới:

Hàm sắp xếp chọn (Selection Sort)

Sắp xếp chọn hay SelectionSort sẽ là thuật toán thứ hai mà mình giới thiệu đến các bạn, ý tưởng của thuật toán này như sau: duyệt từ đầu đến phần tử kề cuối danh sách, duyệt tìm phần tử nhỏ nhất từ vị trí kế phần tử đang duyệt đến hết, sau đó đổi vị trí của phần tử nhỏ nhất đó với phần tử đang duyệt và cứ tiếp tục như vậy.

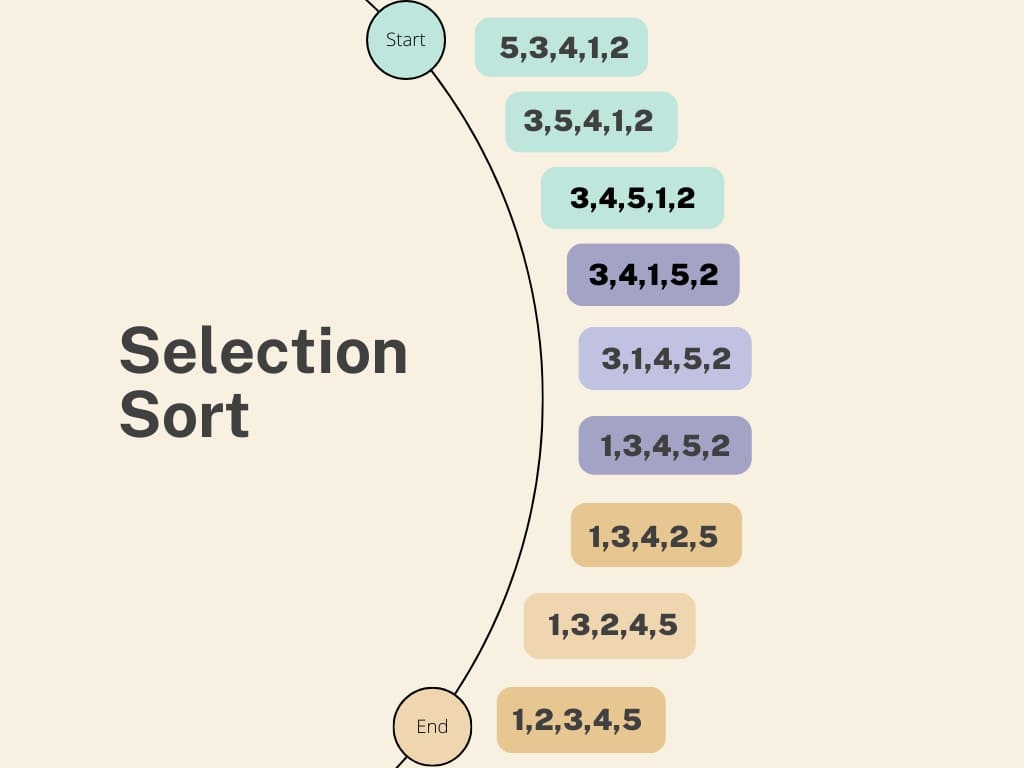
Cho mảng A có n phần tử chưa được sắp xếp. Cụ thể các bước của giải thuật này áp dụng trên mảng A như sau:

Gán i = 0
Gán j = i + 1 và min = A[i]
Nếu j < n:
- Nếu A[j] < A[min] thì min = j
- j = j + 1
- Quay lại bước 3
Đổi chỗ A[min] và A[i]
Nếu i < n – 1:
- Đúng thì i = i + 1 và quay lại bước 2
- Sai thì dừng lại

Ý tưởng và từng bước giải cụ thể đã có, bây giờ mình sẽ sử dụng thuật toán này trong C++:

void SelectionSort(int A[], int n)
{
    int min;
    for (int i = 0; i < n - 1; i++)
    {
        min = i; // tạm thời xem A[i] là nhỏ nhất
        // Tìm phẩn tử nhỏ nhất trong đoạn từ A[i] đến A[n - 1]
        for (int j = i + 1; j < n; j++)
            if (A[j] < A[min]) // A[j] mà nhỏ hơn A[min] thì A[j] là nhỏ nhất
                min = j; // lưu lại vị trí A[min] mới vừa tìm được
        if (min != i) // nếu như A[min] không phải là A[i] ban đầu thì đổi chỗ
            swap(A[i], A[min]);
    }
}

Đối với thuật toán sắp xếp chọn, do sử dụng 2 vòng lặp lồng vào nhau, độ phức tạp thời gian trung bình của thuật toán này là O(n²). Thuật toán sắp xếp chọn mình cài đặt là thuật toán sắp xếp không ổn định, nó còn có một phiên bản khác cải tiến là thuật toán sắp xếp chọn ổn định.

Giải thích ý tưởng thuật toán:

Hàm sắp xếp chèn (Insertion Sort)

Sắp xếp chèn hay insertion sort là thuật toán tiếp theo mà mình giới thiệu, ý tưởng của thuật toán này như sau: ta có mảng ban đầu gồm phần tử A[0] xem như đã sắp xếp, ta sẽ duyệt từ phần tử 1 đến n – 1, tìm cách chèn những phần tử đó vào vị trí thích hợp trong mảng ban đầu đã được sắp xếp.

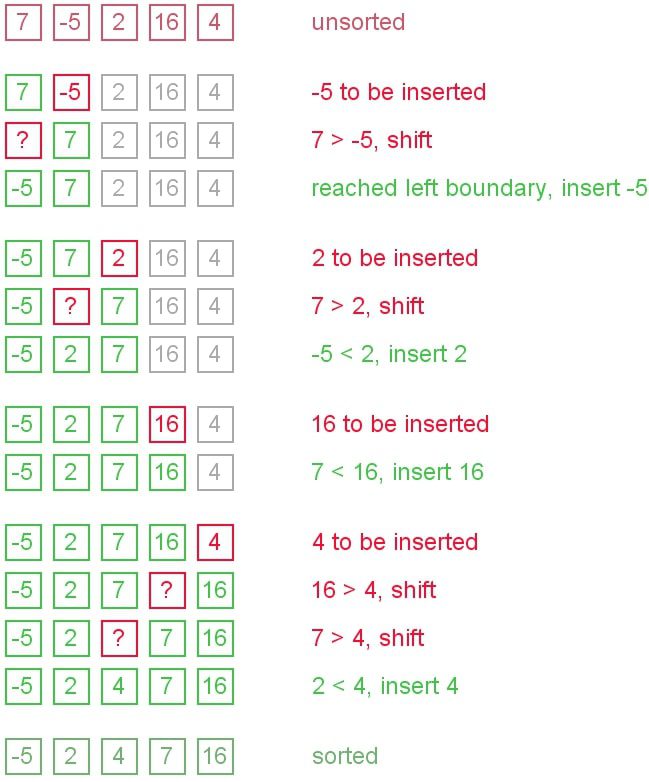
Giả sử cho mảng A có n phần tử chưa được sắp xếp. Các bước thực hiện của thuật toán áp dụng trên mảng A như sau:

Gán i = 1
Gán x = A[i] và pos = i – 1
Nếu pos >= 0 và A[pos] > x:
- A[pos + 1] = A[pos]
- pos = pos – 1
- Quay lại bước 3
A[pos + 1] = x
Nếu i < n:
- Đúng thì i = i + 1 và quay lại bước 2
- Sai thì dừng lại

Bây giờ thì áp dụng nó vào trong C++ thôi!

void InsertionSort(int A[], int n)
{
    int pos, x;
    for (int i = 1; i < n; i++)
    {
        x = A[i]; // lưu lại giá trị của x tránh bị ghi đè khi dịch chuyển các phần tử
        pos = i - 1;
        // tìm vị trí thích hợp để chèn x
        while (pos >= 0 && A[pos] > x)
        {
            // kết hợp với dịch chuyển phần tử sang phải để chừa chỗ cho x
            A[pos + 1] = A[pos];
            pos--;
        }
        // chèn x vào vị trí đã tìm được
        A[pos + 1] = x;
    }
}

Cũng tương tự như sắp xếp chọn, thuật toán sắp xếp chèn cũng có độ phức tạp thời gian trung bình là O(n²) do có hai vòng lặp lồng vào nhau.

Video giải thích ý tưởng thuật toán:

Sắp xếp trộn (Merge Sort)

Sắp xếp trộn (merge sort) là một thuật toán dựa trên kỹ thuật chia để trị, ý tưởng của thuật toán này như sau: chia đôi mảng thành hai mảng con, sắp xếp hai mảng con đó và trộn lại theo đúng thứ tự, mảng con được sắp xếp bằng cách tương tự.

Giả sử left là vị trí đầu và right là cuối mảng đang xét, cụ thể các bước của thuật toán như sau:

Nếu mảng còn có thể chia đôi được (tức left < right)
1. Tìm vị trí chính giữa mảng
2. Sắp xếp mảng thứ nhất (từ vị trí left đến mid)
3. Sắp xếp mảng thứ 2 (từ vị trí mid + 1 đến right)
4. Trộn hai mảng đã sắp xếp với nhau

Bây giờ mình sẽ cài đặt thuật toán cụ thể trong C++ như sau:

// Hàm trộn hai mảng con vào nhau theo đúng thứ tự
void Merge(int A[], int left, int mid, int right)
{
    int n1 = mid - left + 1; // Số phần tử của mảng thứ nhất
    int n2 = right - mid; // Số phần tử của mảng thứ hai

    // Tạo hai mảng tạm để lưu hai mảng con
    int *LeftArr = new int[n1];
    int *RightArr = new int[n2];

    // Sao chép phần tử 2 mảng con vào mảng tạm
    for (int i = 0; i < n1; i++)
        LeftArr[i] = A[left + i];
    for (int i = 0; i < n2; i++)
        RightArr[i] = A[mid + 1 + i];

    // current là vị trí hiện tại trong mảng A
    int i = 0, j = 0, current = left;

    // Trộn hai mảng vào nhau theo đúng thứ tự
    while (i < n1 && j < n2)
        if (LeftArr[i] <= RightArr[j])
            A[current++] = LeftArr[i++];
        else
            A[current++] = RightArr[j++];

    // Nếu mảng thứ nhất còn phần tử thì copy nó vào mảng A
    while (i < n1)
        A[current++] = LeftArr[i++];

    // Nếu mảng thứ hai còn phần tử thì copy nó vào mảng A
    while (j < n2)
        A[current++] = RightArr[j++];

    // Xóa hai mảng tạm đi
    delete[] LeftArr, RightArr;
}

// Hàm chia đôi mảng và gọi hàm trộn
void _MergeSort(int A[], int left, int right)
{
    // Kiểm tra xem còn chia đôi mảng được không
    if (left < right)
    {
        // Tìm phần tử chính giữa
        // left + (right - left) / 2 tương đương với (left + right) / 2
        // việc này giúp tránh bị tràn số với left, right quá lớn
        int mid = left + (right - left) / 2;
 
        // Sắp xếp mảng thứ nhất
        _MergeSort(A, left, mid);
        // Sắp xếp mảng thứ hai
        _MergeSort(A, mid + 1, right);

        // Trộn hai mảng đã sắp xếp
        Merge(A, left, mid, right);
    }
}

// Hàm sắp xếp chính, được gọi khi dùng merge sort
void MergeSort(int A[], int n)
{
    _MergeSort(A, 0, n - 1);
}

Về độ phức tạp, thuật toán Merge Sort có độ phức tạp thời gian trung bình là O(nlog(n)), về không gian, do sử dụng mảng phụ để lưu trữ, và 2 mảng phụ dài nhất là hai mảng phụ ở lần chia đầu tiên có tổng số phần tử bằng đúng số phần tử của mảng nên độ phức tạp sẽ là O(n). Sắp xếp trộn là thuật toán sắp xếp ổn định.

Video minh họa của GeeksforGeeks:

Hàm sắp xếp nhanh (Quick Sort)

Sắp xếp nhanh (quick sort) hay sắp xếp phân đoạn (Partition) là là thuật toán sắp xếp dựa trên kỹ thuật chia để trị, cụ thể ý tưởng là: chọn một điểm làm chốt (gọi là pivot), sắp xếp mọi phần tử bên trái chốt đều nhỏ hơn chốt và mọi phần tử bên phải đều lớn hơn chốt, sau khi xong ta được 2 dãy con bên trái và bên phải, áp dụng tương tự cách sắp xếp này cho 2 dãy con vừa tìm được cho đến khi dãy con chỉ còn 1 phần tử.

Cụ thể áp dụng thuật toán cho mảng như sau:

Chọn một phần tử làm chốt
Sắp xếp phần tử bên trái nhỏ hơn chốt
Sắp xếp phần tử bên phải nhỏ hơn chốt
Sắp xếp hai mảng con bên trái và bên phải pivot

Phần tử được chọn làm chốt rất quan trọng, nó quyết định thời gian thực thi của thuật toán. Phần tử được chọn làm chốt tối ưu nhất là phần tử trung vị, phần tử này làm cho số phần tử nhỏ hơn trong dãy bằng hoặc sấp xỉ số phần tử lớn hơn trong dãy. Tuy nhiên, việc tìm phần tử này rất tốn kém, phải có thuật toán tìm riêng, từ đó làm giảm hiệu suất của thuật toán tìm kiếm nhanh, do đó, để đơn giản, người ta thường sử dụng phần tử chính giữa làm chốt.

Trong bài viết này, mình cũng sẽ sử dụng phần tử chính giữa làm chốt, thuật toán cài đặt trong C++ như sau:

void Partition(int A[], int left, int right)
{
    // Kiểm tra xem nếu mảng có 1 phần tử thì không cần sắp xếp
    if (left >= right)
        return;

    int pivot = A[(left + right) / 2]; // Chọn phần tử chính giữa dãy làm chốt

    // i là vị trí đầu và j là cuối đoạn
    int i = left, j = right;
    while (i < j)
    {
        while (A[i] < pivot) // Nếu phần tử bên trái nhỏ hơn pivot thì ok, bỏ qua
            i++;
        while (A[j] > pivot) // Nếu phần tử bên phải nhỏ hơn pivot thì ok, bỏ qua
            j--;

        // Sau khi kết thúc hai vòng while ở trên thì chắc chắn
        // vị trí A[i] phải lớn hơn pivot và A[j] phải nhỏ hơn pivot
        // nếu i < j
        if (i <= j)
        {
            if (i < j) // nếu i != j (tức không trùng thì mới cần hoán đổi)
                swap(A[i], A[j]); // Thực hiện đổi chổ ta được A[i] < pivot và A[j] > pivot
            i++;
            j--;
        }
    }

    // Gọi đệ quy sắp xếp dãy bên trái pivot
    Partition(A, left, j);
    // Gọi đệ quy sắp xếp dãy bên phải pivot
    Partition(A, i, right);
}

// Hàm sắp xếp chính
void QuickSort(int A[], int n)
{
    Partition(A, 0, n - 1);
}

Thuật toán sắp xếp nhanh không phải là thuật toán sắp xếp ổn định, tuy nhiên vẫn có thể cải tiến nó thành thuật toán sắp xếp ổn định. Độ phức tạp thời gian trung bình của thuật toán này là O(nlog(n)).

Hàm sắp xếp vun đống (Heap Sort)

Heap Sort là một thuật toán sắp xếp dựa trên cấu trúc dữ liệu heap, thường là heap nhị phân. Thuật toán này có độ phức tạp thời gian là O(n log n) và hoạt động tốt với các mảng lớn.

Cách thức hoạt động:

Tạo một max-heap từ mảng đầu vào.
Hoán đổi phần tử gốc của heap với phần tử cuối của mảng.
Giảm kích thước heap bằng cách bỏ qua phần tử cuối cùng đã được sắp xếp.
Điều chỉnh lại heap để duy trì tính chất max-heap.
Lặp lại các bước trên cho đến khi toàn bộ mảng được sắp xếp.

Cú pháp và ví dụ:

#include <iostream>
#include <vector>

void heapify(std::vector<int>& arr, int n, int i) {
    int largest = i; 
    int left = 2 * i + 1; 
    int right = 2 * i + 2; 

    if (left < n && arr[left] > arr[largest])
        largest = left;

    if (right < n && arr[right] > arr[largest])
        largest = right;

    if (largest != i) {
        std::swap(arr[i], arr[largest]);
        heapify(arr, n, largest);
    }
}

void heapSort(std::vector<int>& arr) {
    int n = arr.size();

    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);

    for (int i = n - 1; i > 0; i--) {
        std::swap(arr[0], arr[i]);
        heapify(arr, i, 0);
    }
}

int main() {
    std::vector<int> arr = {12, 11, 13, 5, 6, 7};
    heapSort(arr);

    std::cout << "Sorted array is: \n";
    for (int i = 0; i < arr.size(); i++)
        std::cout << arr[i] << " ";
    std::cout << std::endl;
    return 0;
}

Hàm sắp xếp đếm (Counting Sort)

Counting Sort là một thuật toán sắp xếp không so sánh, có độ phức tạp thời gian là O(n + k) với n là số phần tử và k là phạm vi giá trị của các phần tử. Thuật toán này hiệu quả khi k nhỏ hơn rất nhiều so với n.

Cách thức hoạt động:

Tạo một mảng đếm để lưu số lần xuất hiện của mỗi giá trị trong mảng đầu vào.
Thay đổi mảng đếm để lưu vị trí cuối cùng của mỗi giá trị trong mảng sắp xếp.
Xây dựng mảng kết quả bằng cách đặt các phần tử vào vị trí chính xác của chúng trong mảng đếm.

Cú pháp và ví dụ:

#include <iostream>
#include <vector>

void countingSort(std::vector<int>& arr) {
    int max = *max_element(arr.begin(), arr.end());
    int min = *min_element(arr.begin(), arr.end());
    int range = max - min + 1;

    std::vector<int> count(range), output(arr.size());
    for (int i = 0; i < arr.size(); i++)
        count[arr[i] - min]++;

    for (int i = 1; i < count.size(); i++)
        count[i] += count[i - 1];

    for (int i = arr.size() - 1; i >= 0; i--) {
        output[count[arr[i] - min] - 1] = arr[i];
        count[arr[i] - min]--;
    }

    for (int i = 0; i < arr.size(); i++)
        arr[i] = output[i];
}

int main() {
    std::vector<int> arr = {4, 2, 2, 8, 3, 3, 1};
    countingSort(arr);

    std::cout << "Sorted array is: \n";
    for (int i = 0; i < arr.size(); i++)
        std::cout << arr[i] << " ";
    std::cout << std::endl;
    return 0;
}

Lời kết

Vậy là qua bài viết này, mình đã giới thiệu đến các bạn các thuật toán tìm kiếm phổ biến nhất. Nếu bạn có thắc mắc hoặc góp ý nào, đừng quên để lại bình luận bên dưới bài viết. Đừng quên chia sẻ bài viết này cho bạn bè cùng biết nha. Cảm ơn các bạn đã theo dõi bài viết!

Bài viết gốc được đăng tải tại khiemle.dev

Có thể bạn quan tâm:

Xem thêm các việc làm C++ hấp dẫn tại TopDev

B BenQ RD Series – Dòng Màn Hình Lập Trình 4k+ Đầu Tiên Trên Thế Giới
by Ban Biên Tập TopDev 3 days ago | open comments
i iOS 18 có gì mới? Có nên cập nhật iOS 18 cho iPhone của bạn?
by Ban Biên Tập TopDev 28 days ago | open comments
G Gamma AI là gì? Cách tạo slide chuyên nghiệp chỉ trong vài phút
by Ban biên tập TopDev 29 days ago | open comments
P Power BI là gì? Vì sao doanh nghiệp nên sử dụng PBI?
by Ban Biên Tập TopDev 1 month ago | open comments
K KICC HCMC x TOPDEV – Bước đệm nâng tầm sự nghiệp cho nhân tài IT Việt Nam
by Ban biên tập TopDev 1 month ago | open comments
T Trello là gì? Cách sử dụng Trello để quản lý công việc
by Ban Biên Tập TopDev 1 month ago | open comments
T TOP 10 SỰ KIỆN CÔNG NGHỆ THƯỜNG NIÊN KHÔNG NÊN BỎ LỠ
by Ban biên tập TopDev 1 month ago | open comments
T Tìm hiểu Laptop AI – So sánh Laptop AI với Laptop thường
by Ban biên tập TopDev 1 month ago | open comments
M MySQL vs MS SQL Server: Phân biệt hai RDBMS phổ biến nhất
by Ban Biên Tập TopDev 1 month ago | open comments
S SearchGPT là gì? Công cụ tìm kiếm mới có thể đánh bại Google?
by Ban Biên Tập TopDev 2 months ago | open comments