Ngăn xếp – Stack trong C++ là gì? Cài đặt và sử dụng Ngăn xếp

Bài viết được tổng hợp bởi tác giả Sơn Dương và Khiêm Lê

Khi lập trình, chúng ta thường phải xử lý một lượng lớn dữ liệu thô và chưa được tổ chức. Điều này đỏi hỏi cần một cấu trúc dữ liệu để lưu dữ liệu và cho phép người dùng thao tác trên dữ liệu một cách hiệu quả. Bài viết hôm nay, chúng ta sẽ cùng nhau tìm hiểu một loại cấu trúc dữ liệu rất phổ biến, đó là ngăn xếp stack trong C++.

Ngăn xếp – Stack là gì?

Ngăn xếp Stack là một cấu trúc dữ liệu tuyến tính hoạt động theo nguyên tắc LIFO (Last In First Out), nghĩa là các phần tử được đưa vào ngăn xếp cuối cùng sẽ là phần tử đầu tiên được lấy ra khỏi ngăn xếp.

Bạn có thể hình dung ngăn xếp stack như một chồng sách đặt trong một cái hộp. Khi thêm một sách mới thì nó sẽ được đặt lên trên, cuốn sách cuối cùng được đặt ở trên đỉnh cũng sẽ là cuốn được lấy ra đầu tiên.

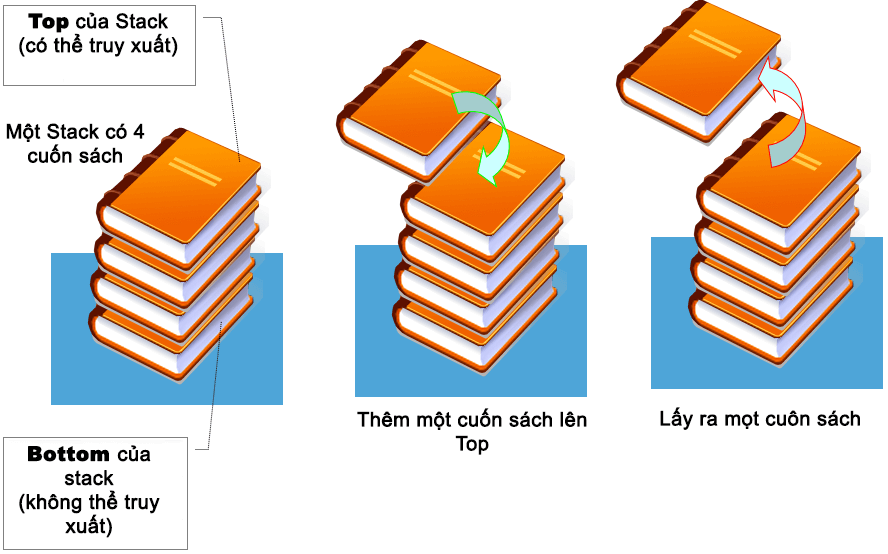
Như bạn thấy ở hình trên, phần tử cuối cùng sẽ là phần tử đầu tiên được lấy ra khỏi ngăn xếp stack.

Stack là một loại container trong thư viện STL ( hiểu đơn giản là dạng thùng chứa dữ liệu).

>> Bài viết liên quan: Queue C++ là gì? Cách cài đặt và sử dụng hàng đợi trong C++

Cách thao tác với Stack C++

Với ngăn xếp stack, chúng ta chỉ có các thao tác xử lý dữ liệu sau:

• push(): Thêm một phần tử mới vào ngăn xếp, số phần tử ngăn xếp tăng lên 1.
• pop(): Xóa một phần tử khỏi stack.
• top(): Trả về giá trị của phần tử trên đỉnh của stack. Số phần tử ngăn xếp không thay đổi.
• size(): Trả về kích thước của ngăn xếp
• isEmpty(): Kiểm tra ngăn xếp stack có rỗng hay không (trả về một giá trị bool true (rỗng) hoặc false (không rỗng).
• isFull(): Kiểm tra trạng thái stack đã đầy hay chưa (trả về một giá trị bool true (đầy) hoặc false (chưa đầy).

Các phương thức trên sẽ đều có độ phức tạp O(1).

>> Xem thêm: Phân biệt ngăn xếp và hàng đợi (Stack vs Queue) trong C++

Cài đặt ngăn xếp Stack trong C/C++

Chúng ta sẽ cùng nhau tìm hiểu cơ chế hoạt động của hai thao tác phổ biến nhất trên stack là Push() và Pop().

struct Node
{
    int data;
    Node *next;
};

Node *CreateNode(int init)
{
    Node *node = new Node;
    node->data = init;
    node->next = NULL;
    return node;
}

struct Stack
{
    Node *head;
};

void CreateStack(Stack &s)
{
    s.head = NULL;
}

int IsEmpty(Stack s)
{
    if (s.head == NULL)
        return 1;
    return 0;
}

• Đầu tiên, kiểm tra stack đã đầy hay chưa. Tức kiểm tra điều kiện tràn
• Trong trường hợp ngăn xếp stack đã đầy, thoát thao tác với thông báo: “Stack đã đầy”.
• Ngược lại, ngăn xếp chưa đầy, con trỏ “top” tăng lên 1, sau đó dữ liệu được thêm vào stack.

Dưới đây là code minh họa cho stack push c++:

void stack_data::push (int a)
{
    if(top >= 5)
    {
        cout << "Overflow\n";
    }
    else
    {
        data[++top] = a; 
    }
}

Tham khảo việc làm C++ Developer hấp dẫn tại TopDev

POP (lấy phần tử trên cùng ra khỏi ngăn xếp)

• Trước tiên, kiểm tra xem ngăn xếp có rỗng hay không.
• Nếu ngăn xếp bị rỗng, thoát thao tác với thông báo: “Ngăn xếp rỗng”.
• Ngược lại, hiển thị giá trị phần tử đang được trỏ bởi con trỏ “top”. Sau đó giảm con trỏ “top” đi 1.

Code minh họa cho thao tác pop

int stack_data::pop ()
{
    if(top < 0)
    {
        cout << "Underflow\n";
        return 0;
    }
    else
    {
        int pop = data[top--];
        return pop;
    }
}

TOP (lấy giá trị phần tử trên cùng ngăn xếp)

Để lấy giá trị phần tử nằm trên cùng ngăn xếp (Top), chúng ta chỉ cần làm tương tự như lấy phần tử trên cùng ra khỏi ngăn xếp, nhưng chúng ta không hủy node đó đi.

int Top(Stack s)
{
    if (IsEmpty(s))
        return 0;
    return s.head->data;
}

Lưu ý: cần phân biệt giữa Pop và Top. Pop là lấy phần tử trên cùng ra khỏi ngăn xếp tức là trả về giá trị phần tử đó và hủy đi. Top chỉ trả về giá trị phần tử trên cùng mà không hủy phần tử đó.

Cuối cùng là chương trình cài đặt stack hoàn thiện như sau:

# include<iostream>
using namespace std;

class stack_data
{
    public:
    int top;
    int data[5]; 
    stack_data()
    {
        top = -1;
    }

    void push (int a);
    int pop ();
    void isEmpty();
    void isFull();
    void display();
};

void stack_data::push (int a)
{
    if(top >= 5)
    {
        cout << "Overflow\n";
    }
    else
    {
        data[++top] = a; 
    }
}

int stack_data::pop ()
{
    if(top < 0)
    {
        cout << "Underflow\n";
        return 0;
    }
    else
    {
        int pop = data[top--];
        return pop;
    }
}

void stack_data::isEmpty()
{
    if(top < 0)
    {
        cout << "Stack Underflow\n";
    }
    else
    {
        cout << "Stack can occupy elements.\n";
    }
}


void stack_data::isFull()
{
    if(top >= 5)
    {
        cout << "Overflow\n";
    }
    else
    {
        cout << "Stack is not full.\n";
    }
}


void stack_data::display()
{
    for(int i=0;i<5;i++)
    {
        cout<<data[i]<<endl;
    }
}

int main() {

    stack_data obj;
    obj.isFull();
    obj.push (40);
    obj.push (99);
    obj.push (66);
    obj.push (40);
    obj.push (11);

    cout<<"Stack after insertion of elements:\n";
    obj.display();

    cout<<"Element popped from the stack:\n";
    cout<<obj.pop ()<<endl;

}

Kết quả khi chạy chương trình trên sẽ như dưới đây:

Stack is not full.
Stack after insertion of elements:
40
99
66
40
11
Element popped from the stack:
11

Ứng dụng của Stack

Tùy vào mỗi yêu cầu cụ thể mà bạn sẽ sử dụng stack để giải quyết. Dưới đây là một số ứng dụng phổ biến của ngăn xếp stack.

• Stack hay được dùng để hoán đổi vị trí của các phần tử trong Array hoặc String.
• Một Stack có thể cần thiết trong tình huống cần Backtracking trong một số thuật toán.
• Trong các ứng dụng kiểu như Text editor, các tính năng undo, redo có thể sẽ cần tới stack.
• Chuyển đổi Infix/Prefix/Postfix trong Binary Trees.

Ứng dụng Stack để xử lý xâu trong C++

Để giải quyết bài toán tính giá trị biểu thức từ một xâu (string) trong C++ sử dụng cấu trúc dữ liệu Stack.

Bài toán: Cho xâu S chỉ gồm các số nguyên dương và các dấu “+”, “-“, “*”, “/” trong S không có dấu khoảng trống. Tính giá trị của biểu thức được biểu diễn bởi S đó.

1. Sử dụng hai stack:

• Một stack để lưu các số (values).
• Một stack để lưu các toán tử (operators).

2. Duyệt qua từng ký tự của xâu S:

• Nếu gặp một số, ta đọc toàn bộ số đó (vì số có thể có nhiều chữ số) và đẩy vào stack values.
• Nếu gặp một toán tử, ta thực hiện các bước sau:
  • Kiểm tra độ ưu tiên của toán tử hiện tại với toán tử ở đỉnh stack operators.
  • Nếu toán tử ở đỉnh stack operators có độ ưu tiên cao hơn hoặc bằng toán tử hiện tại, thì thực hiện phép tính với hai số từ stack values và toán tử từ stack operators.
  • Đẩy toán tử hiện tại vào stack operators.

3. Xử lý phép toán còn lại: Khi duyệt hết xâu S, ta sẽ thực hiện các phép toán còn lại trong stack operators với các số trong stack values.

Code mẫu

#include <iostream>
#include <stack>
#include <string>
#include <cctype>  // For isdigit()

using namespace std;

// Hàm để thực hiện một phép tính cơ bản
int applyOperator(char op, int b, int a) {
    switch (op) {
        case '+': return a + b;
        case '-': return a - b;
        case '*': return a * b;
        case '/': return a / b;
    }
    return 0;
}

// Hàm để xác định độ ưu tiên của toán tử
int precedence(char op) {
    if (op == '+' || op == '-')
        return 1;
    if (op == '*' || op == '/')
        return 2;
    return 0;
}

int evaluateExpression(const string &S) {
    stack<int> values;     // stack để lưu các số
    stack<char> operators; // stack để lưu các toán tử

    for (int i = 0; i < S.length(); i++) {
        if (isdigit(S[i])) {
            int val = 0;
            // Đọc toàn bộ số nguyên (có thể có nhiều chữ số)
            while (i < S.length() && isdigit(S[i])) {
                val = (val * 10) + (S[i] - '0');
                i++;
            }
            values.push(val);
            i--; // Lùi lại một bước vì vòng lặp for sẽ tăng i thêm 1
        } else {
            // Nếu gặp một toán tử, xử lý các phép toán trước đó
            while (!operators.empty() && precedence(operators.top()) >= precedence(S[i])) {
                int val2 = values.top();
                values.pop();

                int val1 = values.top();
                values.pop();

                char op = operators.top();
                operators.pop();

                values.push(applyOperator(op, val2, val1));
            }
            operators.push(S[i]);
        }
    }

    // Thực hiện các phép toán còn lại trong stack
    while (!operators.empty()) {
        int val2 = values.top();
        values.pop();

        int val1 = values.top();
        values.pop();

        char op = operators.top();
        operators.pop();

        values.push(applyOperator(op, val2, val1));
    }

    // Kết quả cuối cùng sẽ nằm trên đỉnh stack values
    return values.top();
}

int main() {
    string S = "3+5*2-8/4";  // Ví dụ: Kết quả là 10
    cout << "Kết quả của biểu thức " << S << " là: " << evaluateExpression(S) << endl;
    return 0;
}

Giải thích

• applyOperator: Hàm này thực hiện phép tính dựa trên toán tử và hai toán hạng.
• precedence: Xác định độ ưu tiên của các toán tử, giúp xử lý đúng thứ tự các phép toán (* / trước, + – sau).
• evaluateExpression: Duyệt qua xâu S, xử lý các số và toán tử theo thứ tự ưu tiên, kết quả cuối cùng sẽ được trả về từ stack values.

Ví dụ: Với xâu S = "3+5*2-8/4", quá trình xử lý sẽ:

• Đầu tiên, 5*2 được thực hiện (do * có độ ưu tiên cao hơn +), sau đó là 8/4, cuối cùng là 3+10-2.
• Kết quả cuối cùng sẽ là 11.

Độ phức tạp của các thao tác trong Stack

Độ phức tạp của push() và pop() là như nhau, đều là: O(1)

Lý do là việc thêm mới và xóa phần tử trong stack đều thực hiện ở một đầu – đỉnh của stack.

Lời kết

Như vậy, trong bài viết này, chúng ta đã hiểu được ngăn xếp stack C++ là gì, cách thức hoạt động cũng như ứng dụng của nó trong lập trình. Mình hi vọng, những kiến thức này sẽ giúp ích cho bạn trong các dự án sắp tới.

Hẹn gặp lại ở bài viết sau nhé.

Có thể bạn quan tâm:

• Giải thích thuật toán Dijkstra – Tìm đường đi ngắn nhất
• Thuật toán tham lam (Greedy Algorithm) – Thực hành với C++
• Top 5 câu hỏi phỏng vấn C++ hay và khó

Đừng bỏ lỡ công việc IT được cập nhật mỗi ngày trên TopDev