Giải thuật Shell Sort và cách triển khai bằng ngôn ngữ lập trình Python

Các giải thuật sắp xếp kinh điển như Bubble Sort, Insertion Sort, Selection Sort hay Quick Sort hẳn không còn xa lạ gì đối với các lập trình viên. Tuy nhiên thực tế trong nhiều bài toán, việc cải tiến các giải thuật trên để áp dụng cho chương trình một cách phù hợp với từng đặc thù dữ liệu tạo ra các giải thuật mới thú vị, Shell Sort là một ví dụ như vậy. Bài viết hôm nay chúng ta cùng nhau tìm hiểu về giải thuật Shell Sort và cách triển khai bằng ngôn ngữ lập trình Python nhé. 

Giải thuật Shell Sort

Shell Sort là một giải thuật sắp xếp được cải tiến từ giải thuật sắp xếp chèn (Insertion Sort), mang lại hiệu quả sắp xếp tốt hơn trong nhiều trường hợp của bài toán thực tế. Ý tưởng chính của thuật toán này là việc khi sử dụng Insertion Sort trong nhiều trường hợp, các giá trị cần đổi chỗ rất nhiều lần, mỗi lần lại chỉ đổi chỗ với phần tử kế bên gây dư thừa các bước chuyển. Ví dụ ở hình dưới, phần tử có giá trị 1 (bé nhất trong dãy) sẽ phải lần lượt đổi chỗ với 6 phần tử nằm trước đó qua 6 bước so sánh mới có thể về đầu danh sách.

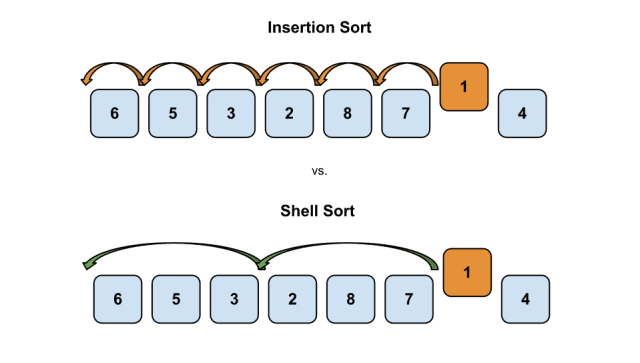
Shell Sort sẽ bắt đầu với việc lựa chọn các phần tử có khoảng cách xa nhau hơn để đổi chỗ, sau đó sẽ thu hẹp khoảng cách lại qua từng bước và cuối cùng trở về khoảng cách bằng 1 (ứng với giải thuật sắp xếp chèn). Như ví dụ ở trên, phần tử có giá trị bằng 1 sẽ chỉ cần trải qua 2 bước so sánh để được chèn về vị trí đầu tiên của mảng.

Khoảng cách giữa các phần tử sẽ thực hiện đổi chỗ trong giải thuật Shell Sort được gọi là khoảng (interval) là số vị trí từ phần tử này đến phần tử khác trong mảng. Có một vài công thức được đưa ra cho việc tính toán khoảng trong Shell Sort, bao gồm:

• • Trình tự nguyên gốc của Shell Sort: N/2 , N/4 , …, 1 với N là số phần tử của mảng
  • Dãy tăng Knuth: 1, 4, 13, …, (3k – 1)/2 với chỉ số k bắt đầu từ 1

• Dãy tăng Hibbard: 1, 3, 7, 15, 31, 63, 127, 255, 511…

• Dãy tăng Papernov & Stasevich: 1, 3, 5, 9, 17, 33, 65,…

• Dãy Pratt: 1, 2, 3, 4, 6, 9, 8, 12, 18, 27, 16, 24, 36, 54, 81….

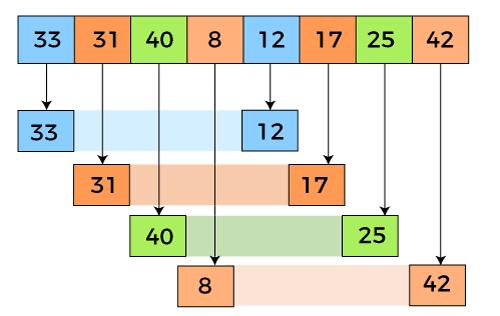
Thuật toán Shell Sort sẽ có hiệu suất sắp xếp phụ thuộc vào dữ liệu đầu vào cùng công thức xác định khoảng được áp dụng. Shell Sort và Insertion Sort có cùng cách thức triển khai thuật toán, chỉ khác nhau ở giá trị khoảng, với Insertion Sort thì giá trị này luôn = 1. Cũng vì thế mà Shell Sort còn được xem là giải thuật tổng quát hóa của Insertion Sort. 

Cách hoạt động của giải thuật

Chúng ta sẽ cùng đi vào cách hoạt động của Shell Sort bằng ví dụ sắp xếp mảng số dưới đây nhé.

Giá trị khoảng cách sử dụng công thức nguyên gốc của Shell Sort. Mảng đầu vào có độ dài N = 8, vì vậy vòng lặp đầu tiên sẽ thực hiện với khoảng = N/2 = 4. Ta sẽ có các cặp giá trị để so sánh và hoán đổi vị trí là {9, 5}, {8, 6}, {3, 4}, và {7, 1}. Kết quả thu được sẽ là:

Tiếp tục giảm giá trị khoảng = N/4 = 2, ta sẽ có được 2 danh sách con gồm {5, 3, 9, 4} và {6, 1, 8, 7}. Việc sắp xếp lúc này thực hiện tương tự như áp dụng Insertion Sort cho từng mảng con ở trên. Kết thúc vòng lặp lần này chúng ta sẽ thu được kết quả:

Cuối cùng, giá trị khoảng sau lần giảm này sẽ về = N/8 = 1. Mảng sẽ được thực hiện sắp xếp chèn một lượt để thu về kết quả đầu ra:

Triển khai giải thuật

Triển khai giải thuật Shell Sort bằng ngôn ngữ lập trình Python như sau:

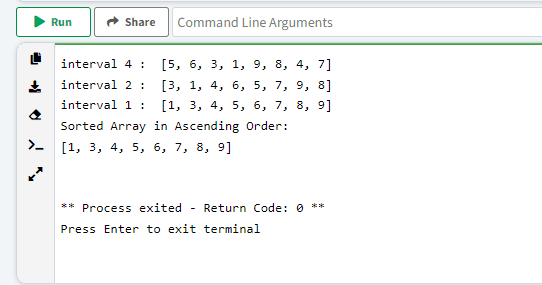
# Shell sort in python
def shellSort(array, n):
    # Rearrange elements at each n/2, n/4, n/8, ... intervals
    interval = n // 2
    while interval > 0:
        for i in range(interval, n):
            temp = array[i]
            j = i
            while j >= interval and array[j - interval] > temp:
                array[j] = array[j - interval]
                j -= interval

            array[j] = temp
        print('interval', interval, ': ', array)
        interval //= 2

data = [9, 8, 3, 7, 5, 6, 4, 1]
size = len(data)
shellSort(data, size)
print('Sorted Array in Ascending Order:')
print(data)

Kết quả console in ra tương ứng các vòng lặp:

Độ phức tạp của giải thuật

Shell Sort cũng như Insertion Sort là những giải thuật không có độ ổn định (Stability) vì nó phụ thuộc lớn vào dữ liệu đầu vào, thời gian chạy có sự chênh lệch lớn giữa trường hợp dữ liệu tốt (Best case) và trường hợp dữ liệu không phù hợp (Worst case). Cụ thể về độ phức tạp thời gian:

• Best: O(nlog n)
• Worst: O(n2)
• Average: O(nlog n), khoảng O(n1.25)

Về bộ nhớ sử dụng, Shell Sort chỉ dùng biến tạm để lưu giá trị lúc hoán đổi vị trí, vì thế độ phức tạp bộ nhớ của thuật toán này là O(1).

Nếu so sánh với Insertion Sort thì Shell Sort không có sự khác biệt nhiều về độ phức tạp ở cả thời gian và bộ nhớ sử dụng. Tuy nhiên như đã nhắc ở đầu bài, giải thuật này cho phép chúng ta tiếp cận theo đặc thù của dữ liệu đầu vào, đưa ra chuỗi giá trị khoảng hợp lý để thực hiện giải thuật. Nhờ đó nó có tính ứng dụng cao trong các bài toán cụ thể khác nhau.

Kết bài

Qua bài viết trên, hy vọng các bạn đã hiểu rõ hơn về giải thuật Shell Sort và có thể dễ dàng triển khai trong nhiều ngôn ngữ lập trình khác nhau. Vận dụng tốt cách thiết lập giá trị khoảng trong Shell Sort sẽ giúp bạn tối ưu hóa việc sắp xếp cho dữ liệu của bài toán mà mình cần giải quyết. Cảm ơn các bạn đã đọc và hẹn gặp lại trong bài viết tiếp theo của mình.

Tác giả: Phạm Minh Khoa

Xem thêm:

• Fuzzy search là gì? Những điều cần biết về thuật toán fuzzy
• Thuật toán Gradient Descent
• Thuật toán Brute Force và bài toán Trapping Rain Water

Tham khảo ngay việc làm IT mọi cấp độ trên TopDev!