Đệ quy là gì? Phương pháp để xây dựng đệ quy

Đệ quy là một khái niệm cơ bản nhưng rất quan trọng trong lập trình hay rộng hơn là trong ngành khoa học máy tính. Việc sử dụng đệ quy sẽ giúp chúng ta giải quyết được rất nhiều bài toán trong thực tế lập trình, vì vậy nó được ứng dụng rất nhiều trong cấu trúc dữ liệu và giải thuật. Bài viết hôm nay chúng ta cùng nhau tìm hiểu xem Đệ quy là gì và các phương pháp để xây dựng đệ quy nhé.

Đệ quy là gì?

Trong toán học và khoa học máy tính, đệ quy – Recursion là một phương pháp giải toán mà trong đó lời giải của bài toán phụ thuộc vào một trường hợp nhỏ hơn của cùng một bài toán đó. Trong lập trình, hàm đệ quy được nhận biết đơn giản là việc trong code thực thi hàm có chứa lời gọi đến chính nó (chính hàm đó).

Ví dụ đơn giản về đệ quy triển khai code bằng ngôn ngữ lập trình JavaScript, trong code triển khai function recursion có chứa đoạn gọi lại chính nó recursion()

function recursion(count) {
  count++;

  if (count <= 5) {
    console.log("step at", count);
    recursion(count);
  }
}

Một hàm đệ quy bao gồm 2 thành phần:

• Phần cơ sở: là trường hợp mà bài toán được giải quyết mà không cần phải gọi lại chính nó. Mục đích của phần cơ sở cũng là việc vòng gặp gọi hàm sẽ được dừng lại tại 1 điều kiện xác định, tránh xảy ra vòng lặp vô hạn.
• Phần đệ quy: là phần xử lý gọi lại hàm, các hành động này sẽ được xử lý gọi liên tiếp cho đến khi lời gọi đến phần cơ sở.

Đệ quy tuyến tính và Đệ quy nhị phân

Trong lập trình nói chung, Đệ quy có thể được chia thành 6 loại, gồm:

• Đệ quy tuyến tính – Linear Recursion
• Đệ quy nhị phân – Binary Recursion
• Đệ quy đuôi – Tail Recursive
• Đệ quy đa tuyến – Exponential Recursive
• Đệ quy lồng – Nested Recursion
• Đệ quy tương hỗ – Mutual Recursion

Các loại đệ quy ở trên đều giống nhau về bản chất đệ quy nhưng có sự khác nhau về số lượng lời gọi đệ quy trong hàm hoặc vị trí của lời gọi. 4 loại đệ quy ở dưới hầu như ít khi được sử dụng trong lập trình mà phần lớn trong nghiên cứu; chúng ta cùng tìm hiểu sâu hơn về đệ quy tuyến tính và nhị phân nhé.

Đệ quy tuyến tính

Là hàm đệ quy chỉ gọi chính nó một lần trong thân hàm. Ví dụ cơ bản nhất là bài toán tính giai thừa n! trong toán học.

Đệ quy nhị phân

Là dạng đệ quy gọi 2 lần chính nó, hay hiểu đơn giản là trong code triển khai sẽ có dòng lệnh gọi đến chính hàm đó 2 lần. Bài toán kinh điển trong trường hợp này chính là dãy Fibonacci.

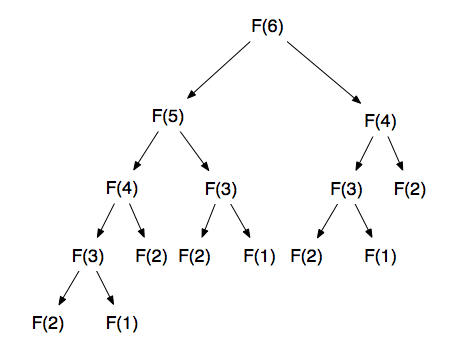
Chúng ta vẫn quen thuộc với công thức tạo ra dãy Fibonacci là: fib(n – 1) + fib(n – 2) từ đó dễ thấy cách triển khai đệ quy nhị phân khi sẽ cần gọi lại 2 lần hàm tính fib. Câu hỏi đặt ra là có thể sử dụng đệ quy tuyến tính cho bài toán Fibonacci này được không? 

Câu trả lời là có, và thậm chí nó sẽ còn tốt hơn về tốc độ so với đệ quy nhị phân. Cách triển khai như dưới đây:

function fib_linearR(a, b, n) {
  if (n <= 2) return b;
  else if (n > 2) return fib_linearR(b, a + b, n - 1);
}

//fib(10) = fib_linearR(1,1,10)

Top việc làm C++ hấp dẫn trên TopDev đang chờ bạn ứng tuyển!

Phương pháp xây dựng đệ quy

Như đã đề cập ở trên, đệ quy bao gồm 2 thành phần là phần cơ sở và phần đệ quy; và để xây dựng đệ quy cũng chính là việc chúng ta đi xác định được logic xử lý và phạm vi của 2 phần này.

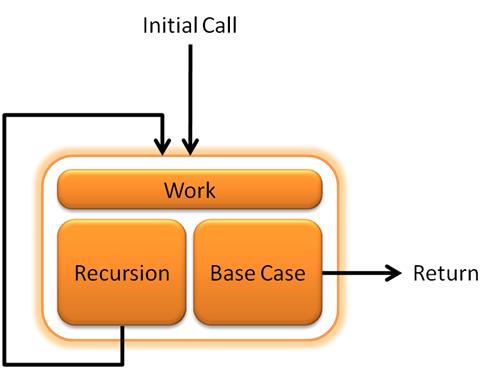
Xác định Base case

Mục tiêu của Base case là trả về một giá trị cụ thể để có thể kết thúc vòng lặp đệ quy. Thông thường trong hầu hết các bài toán thì Base case được xác định cụ thể với giá trị rõ ràng ngay từ đầu. Ví dụ ở bài toán Fibonacci chúng ta có F(1) = 1 và F(2) = 1; hay với bài toán tính giai thừa của một số thì Factorial(1) = 1. 

Base case sẽ không tạo ra hoặc thay đổi các biến, tham số bên ngoài hàm; nó sẽ luôn trả ra một kết quả khi có cùng một đầu vào. Từ đó chúng ta có thể xây dựng Base case là một Pure function, không tạo ra bất kỳ side effect ngoài bên ngoài phạm vi của nó.

Viết logic Đệ quy

Logic đệ quy là việc xác định được khi nào (vị trí) thì gọi lại hàm đệ quy và mỗi lần gọi lại thì vấn đề được thu nhỏ hơn (hay chính là bài toán con). Sau mỗi lần thực hiện gọi lại hàm đệ quy thì bài toán ban đầu sẽ trở nên dễ dàng tính toán hơn và đồng thời đảm bảo được nó sẽ kết thúc vòng lặp vào một trong số các Base case chúng ta đã xây dựng.

Ví dụ như với bài toán Fibonacci, để tính F(5) chúng ta sẽ gọi đến việc tính toán F(4) và F(3) là những bài toán con nhỏ hơn, dễ tính hơn. Và cuối của vòng lặp chúng ta sẽ gọi đến F(2) và F(1) – là những Base case.

Phần đệ quy (Recursion case) rõ ràng sẽ không phải là một Pure Function, nó sẽ sử dụng các tham số ngoài hoặc ít nhất là đọc dữ liệu từ bên ngoài. Hơn nữa, một số bài toán có thể trả về kết quả khác nhau cho cùng một giá trị đầu vào, ví dụ như bài toán tìm đường đi ngắn nhất khi có nhiều lời giải được tìm ra.

Kết bài

Như vậy qua bài viết này chúng ta đã cùng nhau tìm hiểu về Đệ quy, các loại đệ quy và phương pháp để xây dựng đệ quy áp dụng trong lập trình. Đệ quy là một kiến thức cơ bản trong cấu trúc dữ liệu và giải thuật và được áp dụng rất nhiều trong lập trình để giải quyết các bài toán thực tế. Vì vậy hãy nắm vững kiến thức này để có thể sử dụng nó một các hiệu quả nhất nhé. Cảm ơn các bạn đã đọc bài và hẹn gặp lại trong các bài viết tiếp theo của mình.

Tác giả: Phạm Minh Khoa

Xem thêm những bài viết liên quan dưới đây:

• Ứng dụng thuật toán và cấu trúc dữ liệu lúc đi làm
• 8 cấu trúc dữ liệu siêu cơ bản mà Dev nào cũng nên biết
• Thuật toán tìm kiếm nội suy trong JavaScript

Tham khảo thêm các vị trí tuyển dụng ngành IT tại Topdev