8 cấu trúc dữ liệu siêu cơ bản mà Dev nào cũng nên biết – Phần 2: Array và Linked-List, Stack và Queue
Bài viết được cho phép bởi tác giả Phạm Huy Hoàng
Ở phần 1, bọn mình đã ôn lại một số khái niệm như Big-O Notation, Time và Space Complexity rồi. Bạn nào chưa đọc thì đọc lại mới hiểu được trong phần 2 này nha.
Trong phần này, tụi mình sẽ ôn lại những cấu trúc dữ liệu rất cơ bản như Array, LinkedList, Stack and Queue nha!
Mình sẽ giải thích sơ về độ phức tạp, ứng dụng của chúng, cũng như những bài toán các bạn hay gặp với các cấu trúc dữ liệu này nhé.
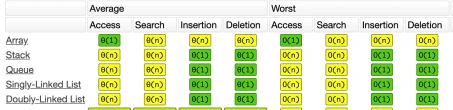
Các bạn tham khảo độ phức tạp của các operation của các CTDL này trong ảnh dưới. Lâu lâu đang đọc mà quên cứ kéo lên xem lại nhé!
Array (Mảng) – Người bạn thân thuộc của lập trình viên
Độ phức tạp
Về bản chất, 1 array là 1 vùng nhớ, gồm nhiều phần tử nằm liền kề nhau.
Dựa vào index i và địa chỉ của phần tử đầu tiên, ta có thể dễ dàng tính ra địa chỉ của phần thử thứ i. Do vậy, ta có thể truy xuất dữ liệu tại vị trí thứ (i) trong array với độ phức tạp (time complexity) là O(1).
Khi array còn chỗ trống, ta cũng có thể dễ dàng thêm phần tử vào array. Thế nhưng, khi array đã đầy, ta không thể thêm phần tử mới. Muốn thêm, ta phải tìm 1 vùng nhớ lớn có thể chứa toàn bộ phần tử, copy toàn array cũ, cộng thêm phần tử mới qua vùng nhớ đó.
Do vậy, thao tác thêm khi array đã đầy sẽ có time complexity và space complexity là O(n). Khi muốn xoá cũng vậy, ta phải bỏ phần tử đó, dồn các phần tử phía sau lên 1 vị trí nên cũng tốn O(n) luôn.
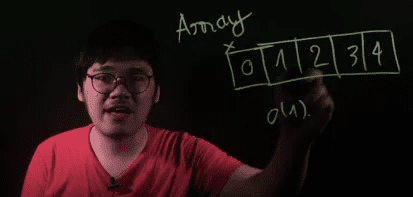
Ứng dụng
Array là một cấu trúc dữ liệu cực kì quen thuộc, học từ trước cả môn cấu trúc dữ liệu. Array được dùng hàng ngày trong công việc, khi ta muốn lưu trữ 1 danh sách nhiều phần tử. Các thuật toán cơ bản như tìm kiếm, sắp xếp đều sử dụng trên array cả.
Note nhẹ: Trong C#, class List cũng sử dụng Array để lưu trữ. Khi array bị đầy, nó sẽ tạo 1 array khác có dung tích gấp đôi array hiện tại, để hạn chế số lần cần tạo array mới.
Một số bài toán hay gặp:
- Các bài toán liên quan đến sắp xếp và tìm kiếm: implement binary search, implement quick sort/merge sort,….
- Tìm tổng toàn bộ các phần tử trong array (các phần tử chẵn, lẻ v…v)
- Đếm số lần xuất hiện của các phần tử, tìm phần tử xuất hiện nhiều nhất
- https://leetcode.com/tag/array
Tham khảo việc làm NodeJS hấp dẫn trên TopDev
Linked List (Danh sách liên kết)
Độ phức tạp
Như đã nói ở phần trên, nhược điểm của array là thêm phần tử mới khá lâu. Do vậy, người ta sáng tạo ra Linked List.
Mỗi phần tử trong Linked List sẽ có 1 con trỏ, trỏ tới phần tử phía sau nó, khi muốn thêm phần tử ta chỉ việc cho phần tử cuối (tail) trỏ tới phần tử mới là được, khi muốn xoá cũng vậy. Do vậy độ phức tạp chỉ là O(1).
Bù lại, việc truy cập sẽ tốn thời gian hơn. Do ta không biết phần tử thử (n) nằm ở đâu, ta phải duyệt qua n phần tử để tìm phần tử đó, time complexity là O(n).
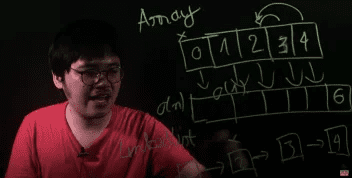
Ứng dụng
LinkedList được dùng khi lưu trữ một danh sách có số lượng phần tử không cố định (dynamic), cần thêm và xoá phần tử. Nếu biết trước số lượng phần tử là cố định, không cần xoá thì cứ dùng array sẽ nhanh hơn.
Linked List có 2 biến thể là Single-linked list và Double-linked list. Với Double-linked list thì 1 phần tử sẽ lưu 2 con trỏ, trỏ về phía trước và phía sau. Tuy tốn bộ nhớ hơn nhưng truy cập tiện hơn.
Một số bài toán hay gặp:
- Đảo ngược 1 linked-list (Không dùng thêm bộ nhớ)
- Xác định linked-list có vòng lặp hay không
- Tìm phần tử nằm giữa linked-list (Chỉ loop 1 lần)
- https://leetcode.com/tag/linked-list
Cặp bài trùng Stack (Ngăn xếp) và Queue (Hàng đợi)
Độ phức tạp
- Stack cho phép ta thêm 1 phần tử lên đầu stack (push), lấy phần tử trên đầu stack ra (pop). Các phần tử nào vào sau sẽ được ra trước, nên gọi là Last In First Out (LIFO)
- Queue thì ngược lại, cho phép ta thêm 1 phần tử vào queue (enqueue), lấy 1 phần tử ra khỏi queue (dequeue). Các phần tử nào vào trước sẽ được ra trước, nên gọi là First In First Out (FIFO)
Hai cấu trúc dữ liệu này cho phép ta thêm/xoá các phần tử dựa theo thứ tự đưa vào, mà không cần phải lưu trữ thời gian. Độ phức tạp của việc đưa vào/lấy ra đều là O(1).

Ứng dụng
- Stack được dùng để implement chức năng Undo/Redo, chức năng Go Back/ Go Next các bạn thấy trên trình duyệt
- Queue được dùng để implement message queue, cho phép các thành phần trong 1 hệ thống trao đổi thông tin
- Queue cũng có 1 số biến thể khác như priority queue hoặc double-ended queue, circulzzar queue
Một số bài toán hay gặp
- Implement queue/stack bằng array hoặc linked listz
- Dùng 2 stack để implement 1 queue (và ngược lại)
- Duyệt các phần tử trong 1 tree (cây) bằng cách dùng stack hoặc queue
- Kiểm tra xem 1 chuỗi có đóng mở ngoặc ({[]}) hợp lý hay không – dùng stack
Tạm kết
Các bạn thấy đấy, 4 cấu trúc dữ liệu trong bài này đều có độ phức tạp O(n) khi tìm kiếm. Để tìm 1 phần tử, ta sẽ phải duyệt qua toàn bộ các phần tử chứa trong mảng/linked-list/stack/queue.
Ở phần sau, mình sẽ giới thiệu về 1 CTDL bá đạo có thể tìm kiếm với độ phức tạp O(1) mang tên HashTable; cùng 1 số những CTDL hay ho nhưng ít gặp như Tree hay Graph nhé!
Bài viết gốc được đăng tải tại toidicodedao
Theo dõi các bài viết liên quan:
- Work Queues trong RabbitMQ
- [Thuật toán] Độ Phức Tạp Không Hề Phức Tạp
- Background job và queue cho nông dân “high tech”
Xem thêm công việc CNTT hấp dẫn trên TopDev
- T Thoughtworks: Nơi công nghệ chạm đích đến
- Đ Đại dương xanh cho Doanh nghiệp tăng trưởng bền vững trên Zalo
- L Lakehouse Architecture: Nền tảng dữ liệu cho ứng dụng AI trong tương lai
- G Giải Quyết Bài Toán Kinh Doanh Bằng Big Data và AI
- B BenQ RD Series – Dòng Màn Hình Lập Trình 4k+ Đầu Tiên Trên Thế Giới
- F Framework nào tốt nhất cho dự án của bạn? – Checklist chi tiết
- K Kinh nghiệm xử lý responsive table hiệu quả
- S Stackoverflow là gì? Bí kíp tận dụng Stack Overflow hiệu quả
- 7 7 kinh nghiệm hữu ích khi làm việc với GIT trong dự án
- B Bài tập Python từ cơ bản đến nâng cao (có lời giải)